Research and academic projects
Rayleigh-Ritz beam bending model
Introduction to computer Methods (CE311K)
This was my final project for my undergraduate civil engineering computer methods course. The Rayleigh - Ritz Method for beams is considered a variational method where deflections are calculated through solving for undetermined coefficients throughout predetermined kinematically admissible functions.
kinematically admissible deflection equations
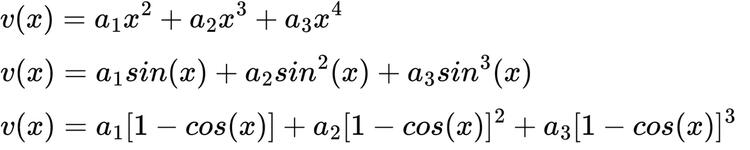
associated boundaries
cantilever
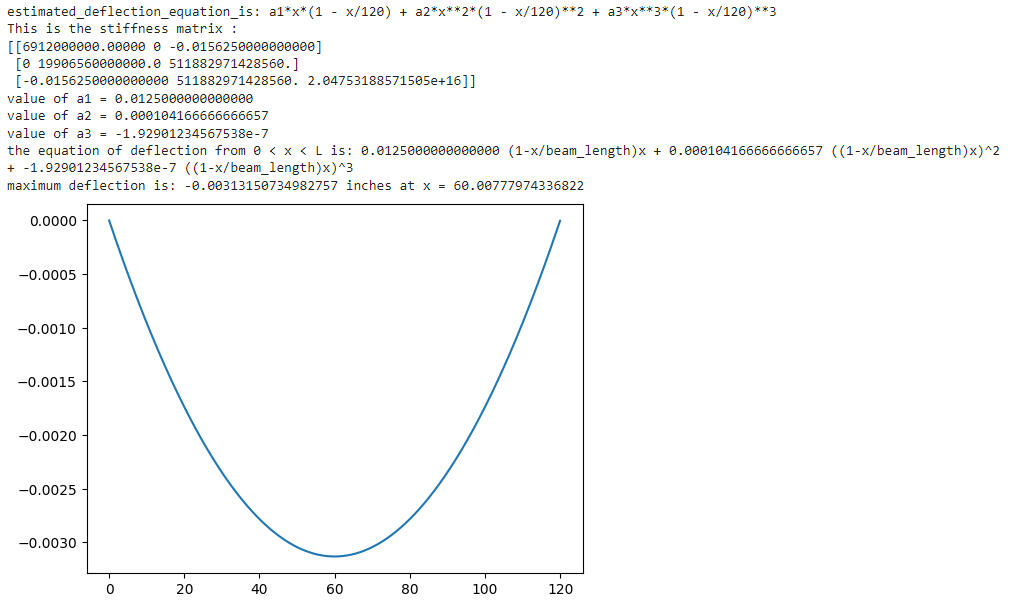
simple supported
fixed-roller support
The undetermined coefficients are solved through minimization of the potential energy of the beam which is given by the equation below.
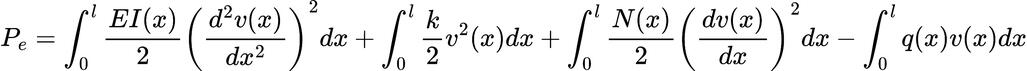
Capability and creation of model
The model was programmed using python and the following packages were used: SymPy SciPy NumPy MatplotLib Math


One of the strength's of the Rayleigh-Ritz method is that it allows for greater flexibility in what parameters can be varied across the entire length of the beam.
In this model, the cross-sectional area of the beam can be varied across its entire length.
Other inputs / adjustable parameters include:
- distributed loads
- varied axial loads
- material (young's modulus)
- beam length
- boundary conditions
Example output and model verification

For a 1' x 1' square cross-sectioned wooden beam:
E = 2 x 106 [psi]
I = 1728 [in4]
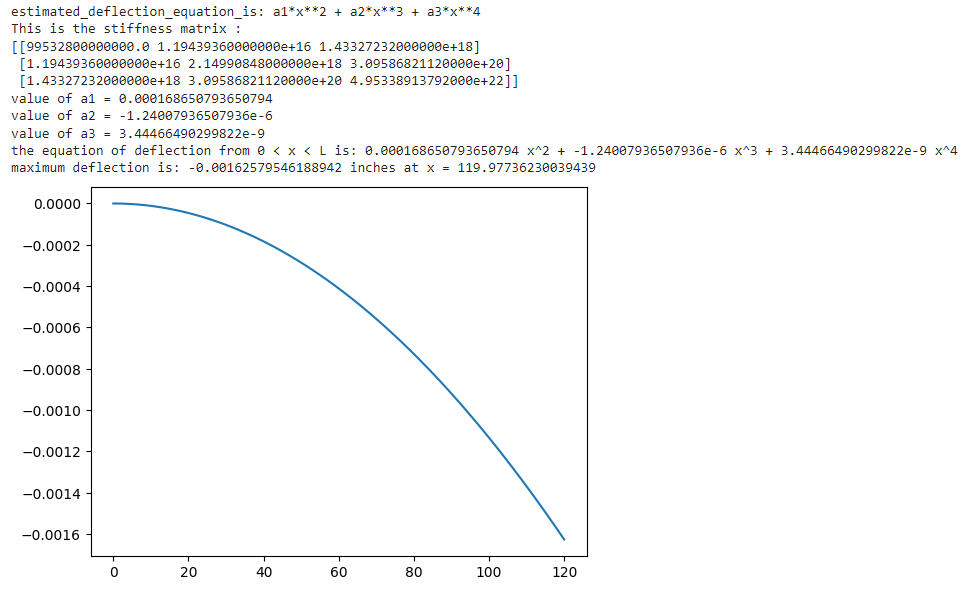
Using the tip-deflection equation: vmax = - WoL4 / 30EI
we obtain that the true deflection is: - 0.001667 inches
The model error is 2.458%